Notice
3.7. Index and suffix trees
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
We have seen with the Boyer-Moore algorithm how we can increase the efficiency of spin searching through the pre-processing of the pattern to be searched. Now we will see that an alternative way of improving the performance is to pre-process the text itself,the searchable text itself and we will, for that, study two methods, the construction of indexes of fixed length words and the algorithm which uses prefix trees. An index of fixed lengthword, what does it mean? Imagine you have a text, a searchable text, that is a text in which you want to search a pattern,here is quite a short text, the sequence is 14 correctors. We will build an index of allthe three letters which appear, a succession of three letters,which appear in the text. Here is the index. Howdoes it work now? Imagine you want to search for occurrences of this triplet, you look up in your index if you can find this triplet. Here and what do you read? You read that this triplet occurred in position Six and Ten. You do not have to make anycomparison on the text because the text has been processed, thisindex table has been built so that immediately from the triplets to be searched for, we can deduce the two positions of interest.
Thème
Documentation
Dans la même collection
-
3.2. A simple algorithm for gene prediction
RechenmannFrançoisBased on the principle we statedin the last session, we will now write in pseudo code a firstalgorithm for locating genes on a bacterial genome. Remember first how this algorithm should work, we first
-
3.5. Making the predictions more reliable
RechenmannFrançoisWe have got a bacterial gene predictor but the way this predictor works is rather crude and if we want to have more reliable results, we have to inject into this algorithmmore biological knowledge. We
-
3.9. Benchmarking the prediction methods
RechenmannFrançoisIt is necessary to underline that gene predictors produce predictions. Predictions mean that you have no guarantees that the coding sequences, the coding regions,the genes you get when applying your
-
3.3. Searching for start and stop codons
RechenmannFrançoisWe have written an algorithm for finding genes. But you remember that we arestill to write the two functions for finding the next stop codonand the next start codon. Let's see how we can do that. We
-
3.6. Boyer-Moore algorithm
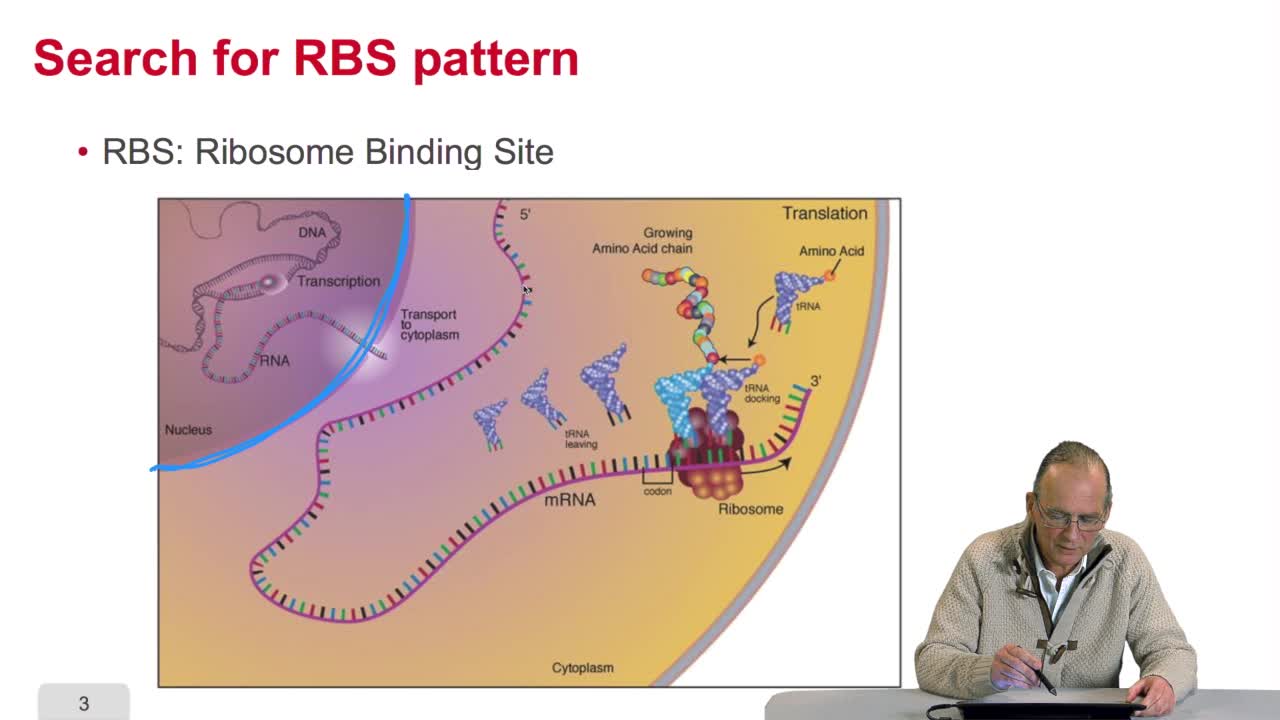
RechenmannFrançoisWe have seen how we can make gene predictions more reliable through searching for all the patterns,all the occurrences of patterns. We have seen, for example, howif we locate the RBS, Ribosome
-
3.1. All genes end on a stop codon
RechenmannFrançoisLast week we studied genes and proteins and so how genes, portions of DNA, are translated into proteins. We also saw the very fast evolutionof the sequencing technology which allows for producing
-
3.10. Gene prediction in eukaryotic genomes
RechenmannFrançoisIf it is possible to have verygood predictions for bacterial genes, it's certainly not the caseyet for eukaryotic genomes. Eukaryotic cells have manydifferences in comparison to prokaryotic cells. You
-
3.4. Predicting all the genes in a sequence
RechenmannFrançoisWe have written an algorithm whichis able to locate potential genes on a sequence but only on one phase because we are looking triplets after triplets. Now remember that the genes maybe located on
-
3.8. Probabilistic methods
RechenmannFrançoisUp to now, to predict our gene,we only rely on the process of searching certain strings or patterns. In order to further improve our gene predictor, the idea is to use, to rely onprobabilistic methods
Avec les mêmes intervenants et intervenantes
-
1.7. DNA walk
RechenmannFrançoisWe will now design a more graphical algorithm which is called "the DNA walk". We shall see what does it mean "DNA walk". Walk on to DNA. Something like that, yes. But first, just have a look again at
-
2.6. Algorithms + data structures = programs
RechenmannFrançoisBy writing the Lookup GeneticCode Function, we completed our translation algorithm. So we may ask the question about the algorithm, does it terminate? Andthe answer is yes, obviously. Is it pertinent,
-
3.3. Searching for start and stop codons
RechenmannFrançoisWe have written an algorithm for finding genes. But you remember that we arestill to write the two functions for finding the next stop codonand the next start codon. Let's see how we can do that. We
-
4.7. Alignment costs
RechenmannFrançoisWe have seen how we can compute the cost of the path ending on the last node of our grid if we know the cost of the sub-path ending on the three adjacent nodes. It is time now to see more deeply why
-
4.9. Recursion can be avoided: an iterative version
RechenmannFrançoisWe have written a recursive function to compute the optimal path that is an optimal alignment between two sequences. Here all the examples I gave were onDNA sequences, four letter alphabet. OK. The
-
1.2. At the heart of the cell: the DNA macromolecule
RechenmannFrançoisDuring the last session, we saw how at the heart of the cell there's DNA in the nucleus, sometimes of cells, or directly in the cytoplasm of the bacteria. The DNA is what we call a macromolecule, that
-
1.10. Overlapping sliding window
RechenmannFrançoisWe have made some drawings along a genomic sequence. And we have seen that although the algorithm is quite simple, even if some points of the algorithmare bit trickier than the others, we were able to
-
2.3. The genetic code
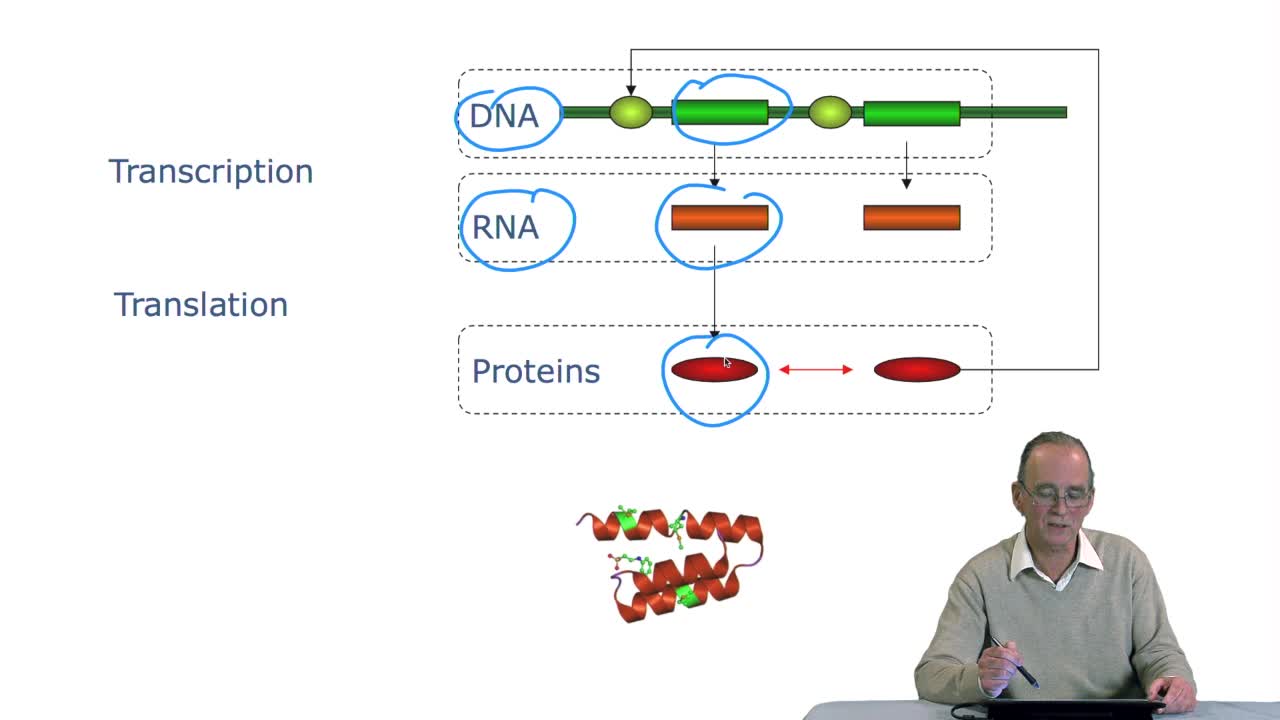
RechenmannFrançoisGenes code for proteins. What is the correspondence betweenthe genes, DNA sequences, and the structure of proteins? The correspondence isthe genetic code. Proteins have indeedsequences of amino acids.
-
3.6. Boyer-Moore algorithm
RechenmannFrançoisWe have seen how we can make gene predictions more reliable through searching for all the patterns,all the occurrences of patterns. We have seen, for example, howif we locate the RBS, Ribosome
-
4.4. Aligning sequences is an optimization problem
RechenmannFrançoisWe have seen a nice and a quitesimple solution for measuring the similarity between two sequences. It relied on the so-called hammingdistance that is counting the number of differencesbetween two
-
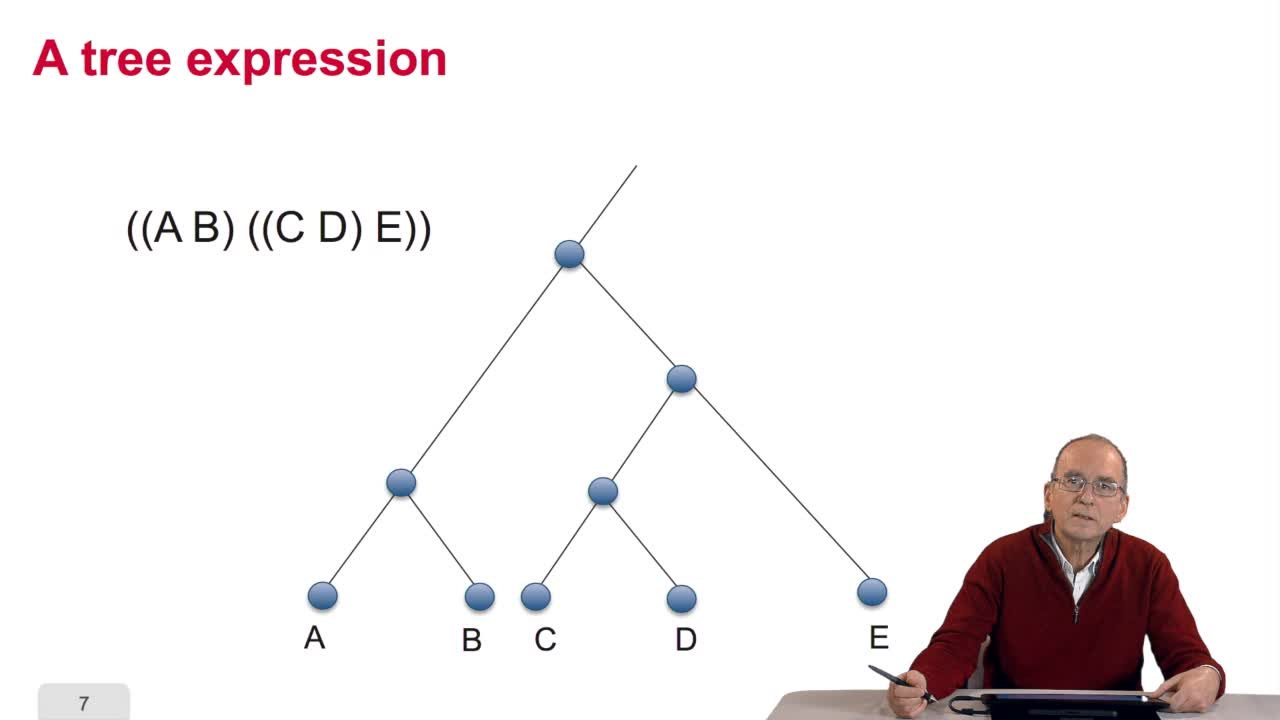
5.2. The tree, an abstract object
RechenmannFrançoisWhen we speak of trees, of species,of phylogenetic trees, of course, it's a metaphoric view of a real tree. Our trees are abstract objects. Here is a tree and the different components of this tree.
-
1.5. Counting nucleotides
RechenmannFrançoisIn this session, don't panic. We will design our first algorithm. This algorithm is forcounting nucleotides. The idea here is that as an input,you have a sequence of nucleotides, of bases, of letters,